Assessing the role that chance may have played in fair tests
The role of chance can lead us to make two types of mistakes when interpreting the results of fair treatment comparisons: we may either mistakenly conclude that there are real differences in treatment outcomes when there are not, or that there are no differences when there are. The larger the number of treatment outcomes of interest observed, the lower the likelihood that we will be misled in these ways.
Because treatment comparisons cannot include everyone who has had or will have the condition being treated, it will never be possible definitively to find the ‘true differences’ between treatments. Instead, studies have to produce best guesses of what the true differences are likely to be.
The reliability of estimated differences will often be indicated by ‘Confidence Intervals’ (CI). These give the range within which the true differences are likely to lie. Most people will already be familiar with the concept of confidence intervals, even if not by that name.
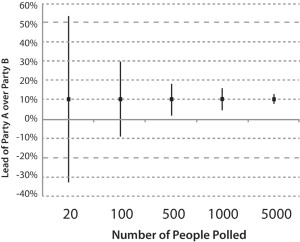
The 95% Confidence Interval (CI) for the difference between Party A and Party B narrows as the number of people polled increases (click to enlarge).
For example, in the run-up to an election, an opinion poll may report that Party A is 10 percentage points ahead of Party B; but the report will then often note that the difference between the parties could be as little as 5 points or as large as 15 points. This ‘confidence interval’ indicates that the true difference between the parties is likely to lie somewhere between 5 and 15 percentage points.
The larger the number of people polled, the less uncertainty there will be about the results, and therefore the narrower will be the confidence interval associated with the estimate of the difference.
Just as one can assess the degree of uncertainty around an estimated difference in the proportions of voters supporting two political parties, so also one can assess the degree of uncertainty around an estimated difference in the proportions of patients improving or deteriorating after two treatments.
And here again, the greater the number of the treatment outcomes observed – say, recovery after a heart attack – in a comparison of two treatments, the narrower will be the confidence intervals surrounding estimates of treatment differences. With confidence intervals, ‘the narrower the better’.
A confidence interval is usually accompanied by an indication of how confident we can be that the true value lies within the range of estimates presented. A ‘95% confidence interval’, for example, means that we can be 95% confident that the true value of whatever it is that is being estimated lies within the confidence interval’s range. This means that there is a 5 in 100 (5%) chance that, actually, the ‘true’ value lies outside the range.
Next: What does a “significant difference” between treatments mean?
